이 글은 A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects 해당 논문에서 Discussion and Experimental Analysis 부분을 보고 작성되었습니다.
A. Activation function
1 ) Discussion of Activation Function
CNN은 복잡한 특징을 표현하기 위해 다양한 활성화 함수를 사용한다.
활성화 함수는 두 신경망 사이에서 출력을 변환시켜 다음 뉴런으로 전달한다.
활성화 함수의 구조는 다음 그림과 같다.
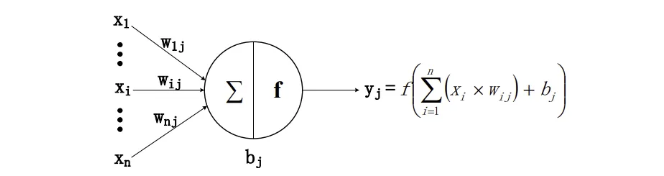
위 그림에서 x_i는 입력을 나타내고 n개의 입력이 뉴런 j에 입력된다.
w_ij는 입력 x_i와 뉴런 j 사이의 가중치 값을 나타내고, b_j는 편향이다.
y_j는 뉴런 j의 출력이다.
f(·)는 활성화 함수로 Sigmoid, Tanh, ReLU 등이 있다.
활성화 함수를 사용하지 않거나 선형 함수를 사용하는 경우, 각 층의 입력은 이전 층의 출력에 대한 선형 함수가 된다.
이 경우, 신경망의 층 수와 상관없이 출력이 선형이 된다.
이는 은닉층이 아무런 효과를 발휘하지 못함을 의미한다.
이러한 이유로 비선형인 활성화 함수가 도입되었다.
활성화 함수를 사용하는 심층 신경망은 비선형 함수가 될 수 있어 우리가 만들고 싶은 임의의 함수를 근사할 수 있다.
이 절에서는 자주 사용되는 활성화 함수에 대해서 논의할 것이다.
Sigmoid 함수는 S자 형태를 가진 전형적인 비선형 활성화 함수중 하나이다.
x 값이 0에 가까워질수록 기울기가 가파르게 변화한다.
Sigmoid 함수는 0~1의 범위를 가지고 있어 이진 분류 문제에 사용될 수 있다.
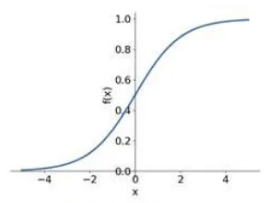
Sigmoid와 달리 Tanh 함수는 -1~1의 범위를 가지고 있다.
Tanh의 평균은 0이므로 일종의 정규화를 적용시키는 것과 같아 다음 층의 학습을 용이하게 한다.

Rectified Linear Unit (ReLU)는 x가 0보다 작으면 0이고, x가 0 이상일 때 함숫값이 x 그 자체가 된다.
Sigmoid 및 Tanh와 비교할 때, ReLU 함수 사용의 장점은 학습 속도를 높일 수 있다는 점이다.
Sigmoid와 Tanh는 미분값을 계산할 때 나눗셈을 요구하는 지수 연산을 포함하는 반면, ReLU의 미분은 상수이다.
또한 Sigmoid와 Tanh의 경우 x 값이 너무 크거나 작으면 함수의 기울기가 너무 작아져 학습이 느리게 수렴할 수 있다.
반면 ReLU는 Sigmoid와 Tanh랑 다르게 gradient vanishing 문제도 해결할 수 있다.
ReLU는 상한을 두지 않지만 ReLU6과 같이 상한을 둘 수도 있다.
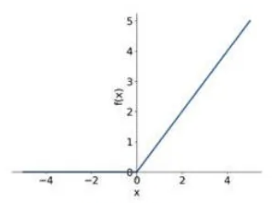
ReLU는 x가 0보다 작을 때 기울기가 0이 되어 오차 역전파를 끊어버린다.
이러한 경우 해당 뉴런은 비활성화되거나 죽은 것으로 간주된다.
이러한 상황을 막기 위해서 개선된 버전이 제안되었다.
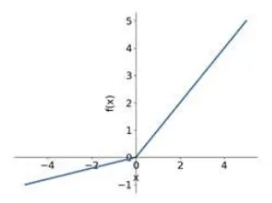
LeakyReLU는 뉴런 비활성화를 줄일 수 있는데, x가 0보다 작을 때 LeakyReLU의 출력은 0이 아닌 x/a가 되며,
여기서 'a'는 (1, +∞) 범위의 하이퍼 파라미터이다.

ReLU의 또 다른 변형인 PReLU는 LeakyReLU와 달리 음수 부분의 기울기가 미리 정해진 값이 아니라 데이터에 기반한다.
Exponential Linear Units (ELU) 함수는 ReLU의 또 다른 개선된 버전이다.
ReLU는 출력의 평균값이 0보다 크다는 문제가 있으며, 이로 인해 다음 층에서 데이터 편향이 발생할 수 있다.
ELU 함수는 음수 값을 가지기 때문에 평균이 0에 가까워져 ReLU보다 수렴 속도가 빠르지만, 음수 부분이 곡선 형태를 띠어 복잡한 미분 계산을 요구한다.

2 ) Experimental Evaluation (실험 평가)
앞서 언급된 활성화 함수를 비교하기 위해, LeNet-5와 VGG-16이라는 두 가지 클래식 CNN 모델을 MNIST, FashionMNIST, CIFAR-10 및 CIFAR-100의 네 가지 데이터 셋에서 테스트했다.
LeNet-5는 처음부터 학습시켰고 VGG-16은 사전 학습된 VGG-16 모델을 기반으로 실험을 진행했다.
두 모델은 다중 분류를 위해 마지막 계층에 softmax를 사용했고, 모든 실험은 Intel Xeon E5-2640 v4 (X2), NVIDIA TITAN RTX (24GB), Python 3.5.6 및 Keras 2.2.4 환경에서 수행되었다.
a ) MNIST & Fashion-MNIST :
MNIST는 10개의 Class로 구성된 필기 숫자 데이터 셋으로, 60,000개의 학습 예제와 10,000개의 테스트 예제로 구성돼 있다.
Fashion-MNIST는 더 복잡한 버전이다.
이 데이터 셋에서 LeNet-5와 VGG-16으로 학습한 결과는 Table I와 아래 사진에 나타나 있다.
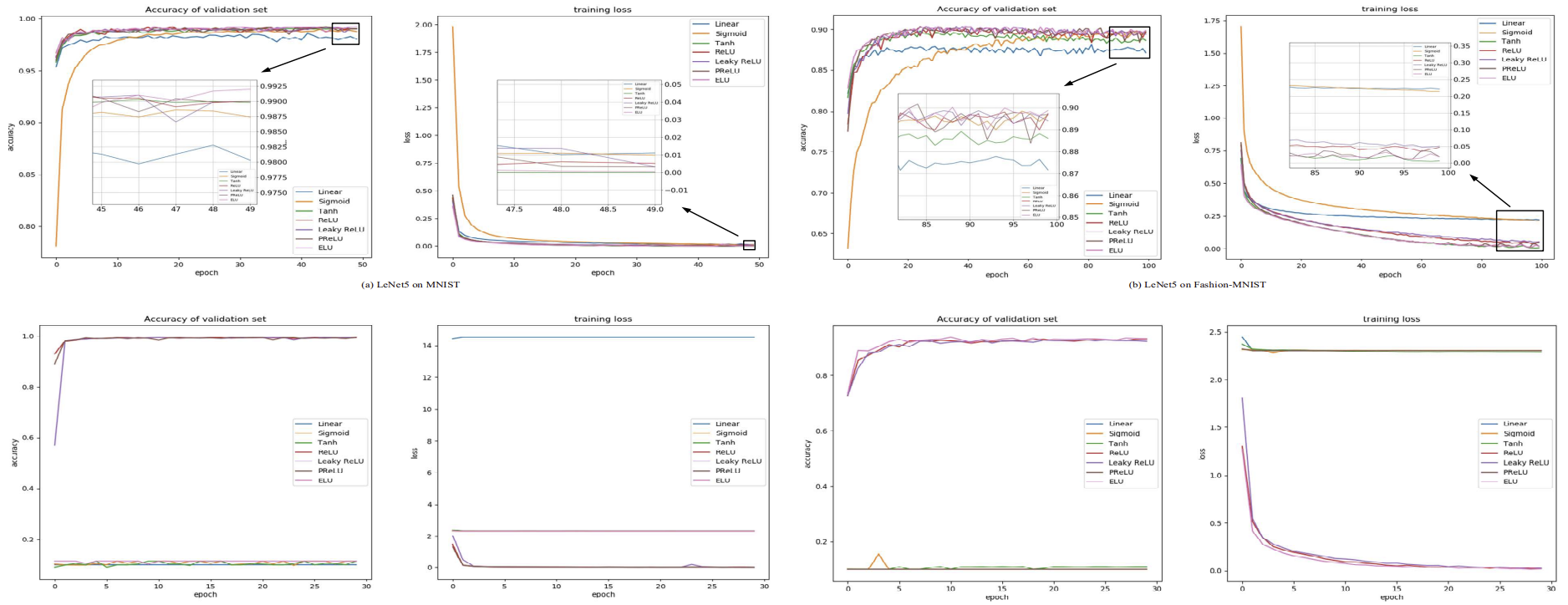
실험 결과로부터 얻은 결론 :
- 선형 함수는 가장 낮은 성능을 보였다 -> 깊은 신경망을 구축할 때 비선형 함수를 추가할 필요성이 있다.
- Sigmoid 함수가 가장 수렴이 느리다. 또한 최종 성능도 뛰어나지 않아 굳이 Sigmoid를 사용할 필요가 없다.
- 정확도 관점에서 ELU가 가장 높은 정확도를 보이나, ReLU, LeakyReLU 및 PReLU보다 약간 개선된 정도이다.
학습 시간 측면에서는, Table I에서 ELU가 ReLU와 LeakyReLU보다 더 시간을 소비하는 경향이 있음이 확인됐다. - ReLU와 LeakyReLU는 PReLU와 ELU에 비해 미분 값이 고정되어 있어 학습 중 안전성이 뛰어나다.
b ) CIFAR-10 & CIFAR-100 :
CIFAR-10 데이터셋은 10개의 Class에 각각 6,000장의 이미지가 포함된 60,000개의 32x32 RGB 이미지로 구성된다.
CIFAR-100은 100개의 Class에 각각 600장의 데이터를 갖는다.
이 데이터 셋에서 LeNet-5와 VGG-16으로 학습한 결과는 Table I와 아래 사진에 나타나 있다.

실험 결과로부터 얻은 결론 :
- Tanh, PReLU 및 ELU 활성화 함수는 학습 말기에 진동(oscillation)을 일으킬 가능성이 높다.
- 사전 학습된 가중치를 사용하는 심층 CNN 모델을 학습시킬 때, Sigmoid 및 Tanh 활성화 함수를 사용하면 수렴하기 어렵다.
- LeakyReLU와 ELU를 사용하여 학습한 모델이 다른 활성화 함수보다 더 나은 정확도를 보인다.
하지만 경우에 따라 ELU는 네트워크가 아무것도 학습하지 못하게 만들 수 있다.
대부분의 경우 LeakyReLU가 정확도와 학습 속도 측면에서 우수한 성능을 보였다.

3 ) Rules of Thumb for Selection
- 이진 분류 문제의 경우 마지막 계층에 Sigmoid를 사용할 수 있으며, 다중 분류 문제의 경우 마지막 계층에 소프트맥스를 사용할 수 있다.
- Sigmoid와 Tanh 함수는 기울기 소실 문제가 일어날 수 있기 때문에 피하는 것이 좋다.
- 활성화 함수를 선택할 아이디어가 없다면, ReLU나 LeakyReLU가 좋은 선택이다.
- 학습 과정에서 많은 뉴런이 비활성화된다면, LeakyReLU, PReLU 등을 활용해 보면 좋다.
- LeakyReLU의 음의 기울기는 학습 속도를 높이기 위해 0.02로 설정할 수 있다.
B. Loss function
손실 함수(loss function)는 예측 값과 실제 값 사이의 거리를 계산하는 데 사용된다.
손실 함수는 학습 기준으로 사용되며, 손실 함수의 출력을 최소화하는 것이 목표이다.
손실 함수로 일반적이게 사용되는 것은 평균 절대 오차(MAE), 평균 제곱 오차(MSE), Cross entropy 등이 있다.
1 ) Loss Function for Regression
CNN에서 회귀 문제를 다룰 때는 MAE 또는 MSE를 사용할 가능성이 높다.
MAE는 예측 값과 실제 값 사이의 절대 오차의 평균을 계산하고
MSE는 이들 사이의 제곱 오차의 평균을 계산한다.
MAE는 이상치(outlier)에 대해 MSE보다 더 견고한 특성을 보인다.
왜냐하면 MSE는 이상치의 제곱 오차를 계산하기 때문이다.
MSE의 결과는 미분이 가능하여 업데이트 속도를 제어할 수 있지만
MAE의 결과는 미분이 불가능하여 업데이트 속도를 제어할 수 없다.
따라서 데이터 집합에 이상치가 많아 모델에 부정적인 영향을 미칠 가능성이 있다면 MAE를 선택하고 아니면 MSE를 고려해야 한다.
2 ) Loss Function for Classification
CNN에서 분류 작업을 수행할 때, 이를 다룰 수 있는 많은 손실 함수가 존재한다.
가장 전형적인 손실 함수 중 하나인 Cross Entropy Loss 함수는 각 클래스에서 예측된 확률과 실제 정답 (0 또는 1)과 비교하고, 이들 간의 차이를 기반으로 페널티 값을 계산한다.
페널티는 로그 함수로 계산되므로, 차이가 작을 경우(예: 0.1 또는 0.2) 낮은 페널티를, 차이가 클 경우(예: 0.9 또는 1.0) 높은 패널티를 받는다.
Cross Entropy Loss는 Softmax Loss라고도 불리는데, 이는 항상 Softmax 계층이 있는 CNN에서 사용된다는 것을 의미한다.
Cross Entropy Loss에는 몇 가지 결함이 있다.
Cross Entropy Loss는 분류의 정확성만을 고려하고, 동일 클래스 내의 응집도나 서로 다른 클래스 간의 경계에 대해서는 신경 쓰지 않는다.
이러한 문제를 해결하기 위해 많은 손실 함수들이 제안되었다.
Contrastive loss는 서로 다른 Class 간의 거리를 확대하고, 동일 Class 내의 거리를 최소화한다.
이는 CNN에서 차원 축소에 사용할 수 있다. 차원 축소 후에도 원래 유사한 두 샘플은 특성 공간에서 여전히 유사하게 유지되며, 반대로 원래 다른 두 샘플은 여전히 다르게 유지된다.
Triplet loss는 세 개의 이미지(anchor이미지, positive 이미지, negative 이미지)로 정의된다.
anchor 이미지와 positive 이미지는 동일 인물에서 얻어진 것이며, nagative 이미지와 anchor 이미지는 서로 다른 인물에서 얻어진 것이다.
Triplet loss를 최소화하는 것은 anchor 이미지와 양성 이미지 간의 거리를 가깝게 하고, anchor 이미지와 nagative 이미지 간의 거리를 멀게 하는 것이다.
Triplet loss는 일반적으로 동일 Class 내에서 개별 인물을 구별해야 하는 세밀한 분류 작업에 컨볼루션 신경망과 함께 사용된다.
Center loss의 목적은 동일 Class 내 분포의 균일성에 집중하는 것이다.
동일 Class의 중심에 고르게 분포되도록 하기 위해, 클래스 내 차이를 최소화하는 추가 제약을 부여한다.
large-margin softmax loss는 같은 클래스 내 응집과 다른 클래스 간 분리를 동시에 달성하는 것이 목적이다.
| 손실 함수 (Loss) | 간단한 설명 (Brief Description) |
| 평균 절대 오차 (Mean absolute error) | 샘플들의 절대 오차 평균을 계산합니다. |
| 평균 제곱 오차 (Mean square error) | 샘플들의 제곱 오차 평균을 계산합니다. |
| 교차 엔트로피 손실 (Cross entropy loss) | 확률 분포와 실제 분포 간의 차이를 계산합니다. |
| 대조 손실 (Contrastive loss) | 서로 다른 범주 간의 거리를 증가시키고, 같은 범주 내에서는 거리를 최소화합니다. |
| 트리플릿 손실 (Triplet loss) | 앵커(Anchor) 샘플과 양성(Positive) 샘플 간의 거리를 최소화하고, 앵커 샘플과 음성(Negative) 샘플 간의 거리를 최대화합니다. |
| 센터 손실 (Center loss) | 동일한 클래스 내에서의 거리를 최소화합니다. |
| 라지 마진 소프트맥스 손실 (Large-margin softmax loss) | 클래스 내 압축과 클래스 간 분리를 동시에 수행합니다. |
3 ) Rules of Thumb for Selection
- CNN 모델을 사용하여 회귀 문제를 다룰 때는 L1 loss (MAE)나 L2 loss (MSE)를 선택할 수 있다.
- 분류 문제를 다룰 때는 나머지 손실 함수들을 사용할 수 있다.
- Cross Entropy Loss는 가장 많이 사용되는 선택지이며, 보통 마지막에 Softmax 계층이 있는 CNN 모델에서 사용된다.
- 만약 클래스 내의 응집도나 서로 다른 클래스 간의 경계가 중요하다면, Cross Entropy Loss를 기반으로 한 개선된 손실 함수들(예: center loss, large-margin softmax loss)을 고려할 수 있다.
- CNN에서의 손실 함수 선택은 사용자의 요구사항에 따라 달라지기도 한다. 예를 들어 얼굴 인식의 경우, 최근에는 contrastive loss와 triplet loss가 자주 사용되는 손실 함수들이다.
C. Optimizer
CNN에서는 비볼록 함수(non-convex function)를 최적화해야 하는 경우가 많다.
직접적인 수학적 최적화 방법은 막대한 연산 능력을 요구하기 때문에,
훈련 과정에서는 최적화 알고리즘(Opimizer)을 사용해서 손실 함수를 줄이고, 짧은 시간 안에 좋은 성능의 모델 파라미터를 찾는 방식을 쓴다.
일반적인 최적화 알고리즘으로는 Momentum, RMSprop, Adam 등이 있다.
1 ) Gradient Descent
CNN 모델을 훈련시키기 위해 사용할 수 있는 경사 하강법(Gradient Descent) 방식에는 크게 세 가지가 있다.
- 배치 경사 하강법(Batch Gradient Descent, BGD)
- 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
- 미니 배치 경사 하강법(Mini-Batch Gradient Descent, MBGD)
BGD는 매번 전체 데이터 배치를 사용해 경사를 계산하여 파라미터를 업데이트한다.
이는 볼록(convex) 함수에서는 Global minima에, 비볼록(non-convex) 함수에서는 Local minima에 수렴함을 보장할 수 있다.
그러나 전체 배치의 평균 경사를 계산해야 하므로 속도가 느리고, 메모리에 적합하지 않은 데이터에는 적용이 어렵다.
따라서 CNN 기반 모델을 훈련할 때는 BGD가 거의 사용되지 않는다.
SGD는 한 번의 업데이트마다 단 하나의 샘플만 사용한다.
한 샘플의 경사만 계산하면 되기 때문에, BGD보다 훨씬 빠르게 업데이트가 가능하다.
이로 인해 SGD는 실시간 학습(online learning)에 적합하다. 하지만 높은 분산을 가진 데이터는 손실 함수가 심하게 진동할 수 있다.
한편으로 이러한 진동이 Local minima를 벗어나 더 나은 지점에 수렴할 수 있다고 하지만, 반면 끝없는 진동으로 인해 수렴하지 못할 수 있다.
BGD와 SGD를 바탕으로 제안된 것이 MBGD이다.
MBGD는 매번 소규모 배치를 사용해 경사를 계산하므로, BGD보다 효율적으로 경사 하강을 수행하면서도, 분산을 줄여 수렴을 더욱 안정적으로 만든다.
이 세 가지 방법 중에서 MBGD가 가장 널리 사용되며, 유명한 CNN 모델들이 많이 사용했다.
예를 들어 AlexNet, VGG, Inception v2, ResNet, DenseNet 등이 있으며, FaceNet, DeepID, DeepID2 등에서도 활용되었다.
2 ) Gradient Descent Optimization Algorithms
MBGD를 기반으로, 모델 학습 속도를 가속화하기 위한 다양한 최적화 알고리즘이 제안되었다.
이 중 일부 주요 알고리즘은 다음과 같다.
모멘텀(Momentum)은 물리적인 운동량을 시뮬레이션하여, 기울기의 지수 가중 평균을 사용해 가중치를 업데이트하는 방식이다. 공이 경사를 타고 내려오는 것과 같이 가중치를 업데이트한다.
특정 차원의 기울기가 다른 차원보다 훨씬 클 경우, 학습 과정이 불균형해질 수 있는데, 모멘텀 알고리즘은 특정 차원에서의 진동을 방지해 더 빠른 수렴을 이룰 수 있도로 한다.
하지만 모멘텀 알고리즘은 경사하강을 맹목적으로 따르는 문제가 있다.
VGG, Inception v1, Residual networks 등의 대표적인 CNN 모델에서 모멘텀을 사용했다.
Nesterove Accelerated Gradient(NAG) 알고리즘은 이러한 모멘텀의 문제를 개선해 예측력을 부여한다.
이는 기울기가 양수가 되기 전에 속도를 줄이게 하며, 다음 위치의 대략적인 기울기를 예측하여 학습률을 미리 조절할 수 있다. NAG는 여러 CNN 기반 작업에서 모델을 훈련시키는 데 사용되었다.
Adagrad 알고리즘은 기울기를 기반으로 한 또 다른 최적화 기법이다.
이는 파라미터마다 학습률을 조절할 수 있으며, 자주 등장하는 특성과 관련된 파라미터는 작은 스텝(낮은 학습률)으로, 드물게 등장하는 특성과 관련된 파라미터는 큰 스텝으로(높은 학습률)으로 업데이트한다. 따라서 희소 데이터(sparse data)를 처리하는데 적합하다.
학습률을 수동으로 조정할 필요가 없는 것이 큰 장점이며, 대부분의 경우 기본값으로 0.01을 사용한다.
Adadelta 알고리즘은 Adagrad의 확장 버전으로, 학습률이 단조롭게 감소하는 문제를 해결하고자 고안됐다.
이 알고리즘은 기울기의 모든 제곱을 누적하는 대신, 고정된 크기의 윈도우(window)를 설정하여 누적 수를 제한한다.
또한, 기울기의 합을 이전 제곱 기울기의 지수 감쇠 평균으로 재귀적으로 정의하여 저장 공간을 줄인다.


RMSprop(Root Mean Square prop) 알고리즘도 Adagrad의 급격히 감소하는 학습률 문제를 해결하기 위해 설계되었다.
자주 사용되는 Adam(Adaptive Moment Esimation)은 모멘텀과 RMSprop을 결합한 알고리즘이다.
Adam은 Adadelta처럼 과거 제곱 기울기의 감쇠 평균과, 모멘텀처럼 과거 기울기의 지수 감쇠 평균을 모두 저장하여 업데이트한다.
AdaMax는 Adam의 변형으로, 학습률의 범위를 보다 단순하게 만들며 모델 학습에 사용되어 왔다.
Nesterov-accelerated Adaptive Moment Estimation(Nadam)은 Adam과 NAG를 결합한 알고리즘이다.
Nadam은 학습률에 대해 더 강한 제약을 가지며, 기울기 업데이트에 직접적인 영향을 준다.
Nadam은 다양한 작업에서 활용되고 있다.
AMSGrad는 Adagrad의 개선 버전이다. AMSGrad 알고리즘의 저자는 Adam 알고리즘의 업데이트 규칙에 오류가 있어, 일부 경우 최적값으로 수렴하지 못하는 문제를 발견했다.
이를 해결하기 위해 AMSGrad는 원래의 지수 평균 대신 과거 제곱 기울기의 최댓값을 사용해 파라미터를 업데이트한다.
3 ) Experimental Evaluation
이번 실험에서는 CIFAR-10 데이터 셋을 활용하여 총 10가지 Optimizer —Mini-Batch Gradient Descent, Momentum, Nesterov, Adagrad, Adadelta, RMSprop, Adam, Adamax, Nadam, AMSGrad—를 테스트했다.
Optimizer는 모두 Mini-Batch를 기반으로 한다.
ImageNet에서 사전 학습된 VGG-16 모델에서 마지막 세 개 층을 제거한 구조를 기반으로 실험을 진행했다.
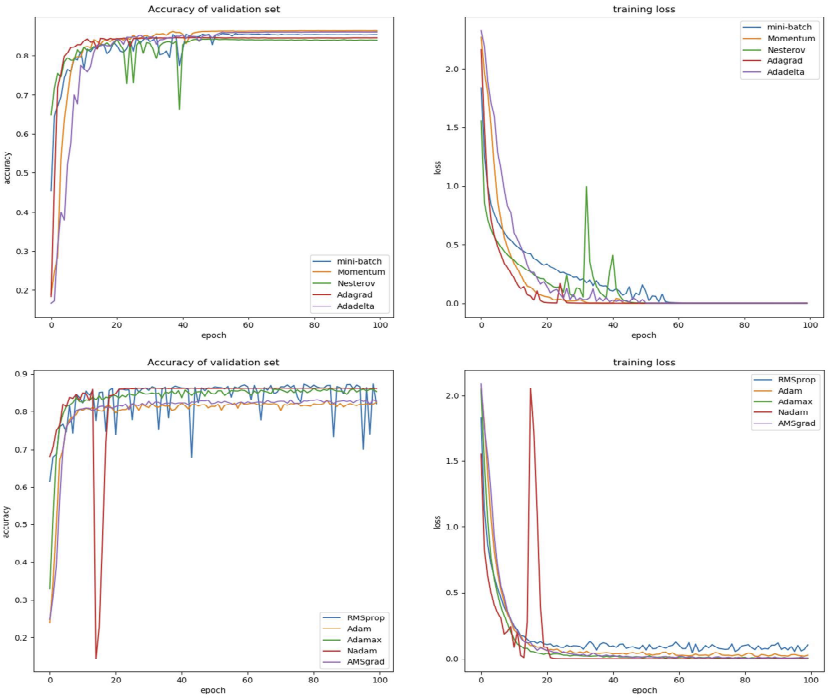
결과는 표 III 및 아래 그림에서 확인할 수 있다.
결론 )
- 대부분의 Optimizer는 CNN 기반 모델이 최종적으로 수렴하도록 할 수 있다.
- Mini-Batch Gradient Descent의 수렴 속도가 가장 느리지만, 결국 수렴은 가능하다.
- NAG, Adagrad, RMSprop, AdaMax, Nadam은 학습 중 진동이 발생하거나 수렴하지 못하는 경우가 있었다.
학습률이 수렴에 큰 영향을 준다는 것을 확인했다. - NAG, RMSprop, Nadam은 진동을 유발할 가능성이 높지만, 이러한 특성이 모델 Local minima에서 벗어나는 데 도움이 될 수 있다.


4 ) Rules of Tumb for Selection
- 연산 비용과 각 업데이트의 정확도 간의 균형을 맞추기 위해 Mini-Batch를 사용하는 것이 좋다.
- 옵티마이저의 성능은 데이터 분포와 밀접한 관련이 있으므로, 앞서 언급한 다양한 옵티마이저들을 자유롭게 시도해 보는 것이 좋다.
- 과도한 진동이나 발산 현상이 발생할 경우, 학습률을 낮추는 것이 좋은 선택이 될 수 있다.